函数题
6-1 Deque
A “deque” is a data structure consisting of a list of items, on which the following operations are possible:
- Push(X,D): Insert item X on the front end of deque D.
- Pop(D): Remove the front item from deque D and return it.
- Inject(X,D): Insert item X on the rear end of deque D.
- Eject(D): Remove the rear item from deque D and return it. Write routines to support the deque that take O(1) time per operation.
Format of functions:
Deque CreateDeque();
int Push( ElementType X, Deque D );
ElementType Pop( Deque D );
int Inject( ElementType X, Deque D );
ElementType Eject( Deque D );
where Deque is defined as the following:
typedef struct Node *PtrToNode;
struct Node {
ElementType Element;
PtrToNode Next, Last;
};
typedef struct DequeRecord *Deque;
struct DequeRecord {
PtrToNode Front, Rear;
};
Here the deque is implemented by a doubly linked list with a header. Front and Rear point to the two ends of the deque respectively. Front always points to the header. The deque is empty when Front and Rear both point to the same dummy header.
Note: Push and Inject are supposed to return 1 if the operations can be done successfully, or 0 if fail. If the deque is empty, Pop and Eject must return ERROR which is defined by the judge program.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
#define ElementType int
#define ERROR 1e5
typedef enum { push, pop, inject, eject, end } Operation;
typedef struct Node *PtrToNode;
struct Node {
ElementType Element;
PtrToNode Next, Last;
};
typedef struct DequeRecord *Deque;
struct DequeRecord {
PtrToNode Front, Rear;
};
Deque CreateDeque();
int Push( ElementType X, Deque D );
ElementType Pop( Deque D );
int Inject( ElementType X, Deque D );
ElementType Eject( Deque D );
Operation GetOp(); /* details omitted */
void PrintDeque( Deque D ); /* details omitted */
int main()
{
ElementType X;
Deque D;
int done = 0;
D = CreateDeque();
while (!done) {
switch(GetOp()) {
case push:
scanf("%d", &X);
if (!Push(X, D)) printf("Memory is Full!\n");
break;
case pop:
X = Pop(D);
if ( X==ERROR ) printf("Deque is Empty!\n");
break;
case inject:
scanf("%d", &X);
if (!Inject(X, D)) printf("Memory is Full!\n");
break;
case eject:
X = Eject(D);
if ( X==ERROR ) printf("Deque is Empty!\n");
break;
case end:
PrintDeque(D);
done = 1;
break;
}
}
return 0;
}
/* Your function will be put here */
Sample Input:
Pop
Inject 1
Pop
Eject
Push 1
Push 2
Eject
Inject 3
End
Sample Output:
Deque is Empty!
Deque is Empty!
Inside Deque: 2 3
参考答案
Deque CreateDeque()
{
// 创建双向链表
Deque deque = (Deque)malloc(sizeof(struct DequeRecord));
if(deque == NULL) return NULL;
// 创建Deque中的节点,头节点
PtrToNode head_node = (PtrToNode)malloc(sizeof(struct Node));
if(head_node == NULL)
{
free(deque);
return NULL;
}
head_node->Next = NULL;
head_node->Last = NULL;
deque->Front = head_node;
deque->Rear = head_node;
return deque;
}
// 入队,成功返回1,失败返回0
int Push(ElementType X, Deque D )
{
// 创建要插入的节点
PtrToNode push_node = (PtrToNode)malloc(sizeof(struct Node));
if(push_node == NULL) return 0;
// 将X保存到节点中,并将节点插入到头节点之后
push_node->Element = X;
push_node->Next = D->Front->Next;
push_node->Last = D->Front;
// 非空链表插入处理
// 将原本首元节点(如果存在)的前向指针指向当前节点
if(push_node->Next != NULL)
{
push_node->Next->Last = push_node;
}
// 空链表插入处理
else
{
D->Rear = push_node;
}
// 修改D的首元节点指针指向
D->Front->Next = push_node;
return 1;
}
// 出队,成功返回出队元素,并从队列中移除该元素,失败返回ERROR
ElementType Pop( Deque D )
{
// 空队处理
if(D->Front == D->Rear) return ERROR;
// 非空队处理
// 保存队头元素
PtrToNode pop_node = D->Front->Next;
ElementType element = pop_node->Element;
D->Front->Next = pop_node->Next;
// 从队列中删除该元素,删除后是否为空队,两种处理情况
// 队列不止一个节点
if(pop_node->Next != NULL)
{
pop_node->Next->Last = D->Front;
}
// 队列仅有一个节点
else
{
// Front永远指向头节点,Rear指向头节点
D->Rear = D->Front;
}
// 释放该节点
free(pop_node);
return element;
}
// 将X插入到D的末尾
int Inject( ElementType X, Deque D )
{
// 创建要插入的节点
PtrToNode inject_node = (PtrToNode)malloc(sizeof(struct Node));
if(inject_node == NULL) return 0;
inject_node->Element = X;
// 因为头节点的存在,所以不论是空队还是非空队,都只需要将节点连接在Rear节点之后即可
inject_node->Next = NULL;
inject_node->Last = D->Rear;
D->Rear->Next = inject_node;
D->Rear = inject_node;
return 1;
}
// 移出末尾节点
ElementType Eject( Deque D )
{
// 空队处理
if(D->Front == D->Rear) return ERROR;
// 非空队处理
PtrToNode eject_node = D->Rear;
ElementType element = eject_node->Element;
D->Rear = eject_node->Last;
eject_node->Last->Next = NULL;
free(eject_node);
return element;
}
// 队头出队入队后 需要考虑 空队 和 非空队 是因为空队时需要修改Rear,非空队时不需要修改Rear
// 而队尾出队入队后 一定只需要处理Rear,Front永远指向头节点,不用处理
6-2 Two Stacks In One Array
Write routines to implement two stacks using only one array. Your stack routines should not declare an overflow unless every slot in the array is used.
Format of functions:
Stack CreateStack( int MaxElements );
int IsEmpty( Stack S, int Stacknum );
int IsFull( Stack S );
int Push( ElementType X, Stack S, int Stacknum );
ElementType Top_Pop( Stack S, int Stacknum );
where int Stacknum is the index of a stack which is either 1 or 2; int MaxElements is the size of the stack array; and Stack is defined as the following:
typedef struct StackRecord *Stack;
struct StackRecord {
int Capacity; /* maximum size of the stack array */
int Top1; /* top pointer for Stack 1 */
int Top2; /* top pointer for Stack 2 */
ElementType *Array; /* space for the two stacks */
}
Note: Push is supposed to return 1 if the operation can be done successfully, or 0 if fails. If the stack is empty, Top_Pop must return ERROR which is defined by the judge program.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
#define ERROR 1e8
typedef int ElementType;
typedef enum { push, pop, end } Operation;
typedef struct StackRecord *Stack;
struct StackRecord {
int Capacity; /* maximum size of the stack array */
int Top1; /* top pointer for Stack 1 */
int Top2; /* top pointer for Stack 2 */
ElementType *Array; /* space for the two stacks */
};
Stack CreateStack( int MaxElements );
int IsEmpty( Stack S, int Stacknum );
int IsFull( Stack S );
int Push( ElementType X, Stack S, int Stacknum );
ElementType Top_Pop( Stack S, int Stacknum );
Operation GetOp(); /* details omitted */
void PrintStack( Stack S, int Stacknum ); /* details omitted */
int main()
{
int N, Sn, X;
Stack S;
int done = 0;
scanf("%d", &N);
S = CreateStack(N);
while ( !done ) {
switch( GetOp() ) {
case push:
scanf("%d %d", &Sn, &X);
if (!Push(X, S, Sn)) printf("Stack %d is Full!\n", Sn);
break;
case pop:
scanf("%d", &Sn);
X = Top_Pop(S, Sn);
if ( X==ERROR ) printf("Stack %d is Empty!\n", Sn);
break;
case end:
PrintStack(S, 1);
PrintStack(S, 2);
done = 1;
break;
}
}
return 0;
}
/* Your function will be put here */
Sample Input:
5
Push 1 1
Pop 2
Push 2 11
Push 1 2
Push 2 12
Pop 1
Push 2 13
Push 2 14
Push 1 3
Pop 2
End
Sample Output:
Stack 2 is Empty!
Stack 1 is Full!
Pop from Stack 1: 1
Pop from Stack 2: 13 12 11
参考答案
// 创建共享栈,两栈共享同一数组空间
Stack CreateStack(int MaxElements)
{
// 申请栈控制结构的内存
Stack stack = (Stack)malloc(sizeof(struct StackRecord));
// 申请栈数组的内存空间(两个栈共享)
stack->Array = (ElementType *)malloc(sizeof(ElementType) * MaxElements);
// 记录数组总容量
stack->Capacity = MaxElements;
// 栈1初始化:从数组头部开始,空栈时top指针为-1
stack->Top1 = -1;
// 栈2初始化:从数组尾部开始,空栈时top指针为数组末尾后一位置
stack->Top2 = MaxElements;
return stack;
}
// 判断指定栈是否为空
int IsEmpty(Stack S, int Stacknum)
{
if (Stacknum == 1)
// 栈1为空的条件:top指针处于初始-1位置
return S->Top1 == -1;
if (Stacknum == 2)
// 栈2为空的条件:top指针处于初始Capacity位置
return S->Top2 == S->Capacity;
// 处理异常栈编号(根据题意实际不会执行到这里)
return ERROR;
}
// 判断共享数组是否已满
int IsFull(Stack S)
{
// 当栈1的下个插入位置(top+1)与栈2的下个插入位置(top-1)相遇时数组满
return S->Top1 + 1 == S->Top2;
}
// 元素入栈操作
int Push(ElementType X, Stack S, int Stacknum)
{
if (Stacknum != 1 && Stacknum != 2) return 0;
if(IsFull(S)) return 0; // 前置检查数组是否已满
switch (Stacknum)
{
case 1:
// 栈1:先移动top指针再写入(前置++保证先移动到新位置)
S->Array[++S->Top1] = X;
break;
case 2:
// 栈2:先移动top指针再写入(前置--保证先移动到新位置)
S->Array[--S->Top2] = X;
break;
default:
return ERROR; // 处理异常栈编号
}
return 1; // 入栈成功
}
// 获取栈顶元素并出栈
ElementType Top_Pop(Stack S, int Stacknum)
{
if (Stacknum != 1 && Stacknum != 2) return ERROR;
if(IsEmpty(S,Stacknum)) return ERROR; // 前置检查栈空
switch (Stacknum)
{
case 1:
// 栈1:先取当前元素,再移动top指针(后置--)
return S->Array[S->Top1--];
case 2:
// 栈2:先取当前元素,再移动top指针(后置++)
return S->Array[S->Top2++];
default:
return ERROR; // 处理异常栈编号
}
}
6-3 Add Two Polynomials
Write a function to add two polynomials. Do not destroy the input. Use a linked list implementation with a dummy head node. Note: The zero polynomial is represented by an empty list with only the dummy head node.
Format of functions:
Polynomial Add( Polynomial a, Polynomial b );
where Polynomial is defined as the following:
typedef struct Node *PtrToNode;
struct Node {
int Coefficient;
int Exponent;
PtrToNode Next;
};
typedef PtrToNode Polynomial;
/* Nodes are sorted in decreasing order of exponents.*/
The function Add is supposed to return a polynomial which is the sum of a and b.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
typedef struct Node *PtrToNode;
struct Node {
int Coefficient;
int Exponent;
PtrToNode Next;
};
typedef PtrToNode Polynomial;
Polynomial Read(); /* details omitted */
void Print( Polynomial p ); /* details omitted */
Polynomial Add( Polynomial a, Polynomial b );
int main()
{
Polynomial a, b, s;
a = Read();
b = Read();
s = Add(a, b);
Print(s);
return 0;
}
/* Your function will be put here */
Sample Input:
4
3 4 -5 2 6 1 -2 0
3
5 20 -7 4 3 1
Sample Output:
5 20 -4 4 -5 2 9 1 -2 0
参考答案
// 两个多项式求和,指数相同,系数相加
// 给的例子是从高次到低次
Polynomial Add( Polynomial a, Polynomial b )
{
// 不写这个也对,因为后续没有修改a和b链表,如果后续修改a和b链表,会同时影响main中的s,所以不写其实更好
// if(a->Next == NULL) return b;
// if(b->Next == NULL) return a;
// 例子是高次到低次,先假设都是这样的
PtrToNode a_temp = a->Next;
PtrToNode b_temp = b->Next;
Polynomial result = (Polynomial)malloc(sizeof(struct Node));
result->Next = NULL;
PtrToNode r_tail = result;
// 都不为空的时候进行加法运算
while (a_temp && b_temp)
{
if(a_temp->Exponent == b_temp->Exponent)
{
PtrToNode newNode = (PtrToNode)malloc(sizeof(struct Node));
newNode->Coefficient = a_temp->Coefficient + b_temp->Coefficient;
if(newNode->Coefficient != 0)
{
newNode->Exponent = a_temp->Exponent;
newNode->Next = NULL;
r_tail->Next = newNode;
r_tail = newNode;
}
a_temp = a_temp->Next;
b_temp = b_temp->Next;
}
else if(a_temp->Exponent > b_temp->Exponent)
{
PtrToNode newNode = (PtrToNode)malloc(sizeof(struct Node));
newNode->Coefficient = a_temp->Coefficient;
newNode->Exponent = a_temp->Exponent;
newNode->Next = NULL;
r_tail->Next = newNode;
r_tail = newNode;
a_temp = a_temp->Next;
}
else if(b_temp->Exponent > a_temp->Exponent)
{
PtrToNode newNode = (PtrToNode)malloc(sizeof(struct Node));
newNode->Coefficient = b_temp->Coefficient;
newNode->Exponent = b_temp->Exponent;
newNode->Next = NULL;
r_tail->Next = newNode;
r_tail = newNode;
b_temp = b_temp->Next;
}
}
// 剩余a的情况下,复制a到result
while(a_temp)
{
PtrToNode newNode = (PtrToNode)malloc(sizeof(struct Node));
newNode->Coefficient = a_temp->Coefficient;
newNode->Exponent = a_temp->Exponent;
newNode->Next = NULL;
r_tail->Next = newNode;
r_tail = newNode;
a_temp = a_temp->Next;
}
// 剩余b的情况下,复制b到result
while(b_temp)
{
PtrToNode newNode = (PtrToNode)malloc(sizeof(struct Node));
newNode->Coefficient = b_temp->Coefficient;
newNode->Exponent = b_temp->Exponent;
newNode->Next = NULL;
r_tail->Next = newNode;
r_tail = newNode;
b_temp = b_temp->Next;
}
return result;
}
6-4 Reverse Linked List
Write a nonrecursive procedure to reverse a singly linked list in O(N) time using constant extra space.
Format of functions:
List Reverse( List L );
where List is defined as the following:
typedef struct Node *PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
struct Node {
ElementType Element;
Position Next;
};
The function Reverse is supposed to return the reverse linked list of L, with a dummy header.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
typedef struct Node *PtrToNode;
typedef PtrToNode List;
typedef PtrToNode Position;
struct Node {
ElementType Element;
Position Next;
};
List Read(); /* details omitted */
void Print( List L ); /* details omitted */
List Reverse( List L );
int main()
{
List L1, L2;
L1 = Read();
L2 = Reverse(L1);
Print(L1);
Print(L2);
return 0;
}
/* Your function will be put here */
Sample Input:
5
1 3 4 5 2
Sample Output:
2 5 4 3 1
2 5 4 3 1
参考答案
// 观察题目以及代码得知,为原地反转链表,而不是新建链表头插保存反转
List Reverse(List L)
{
if (L == NULL || L->Next == NULL) return L; // 处理空链表情况
Position current = L->Next; // 当前节点,从第一个节点开始
Position last = NULL; // 上一个节点
Position next = NULL; // 下一个节点
while (current != NULL)
{
next = current->Next; // 先保存下一个节点
current->Next = last; // 反转指针
last = current; // 上一个指针前移
current = next; // 当前指针前移
}
// 当current为空时,last为最后一个节点
L->Next = last;
return L;
}
6-5 Evaluate Postfix Expression
Write a program to evaluate a postfix expression. You only have to handle four kinds of operators: +, -, x, and /.
Format of functions:
ElementType EvalPostfix( char *expr );
where expr points to a string that stores the postfix expression. It is guaranteed that there is exactly one space between any two operators or operands.
The function EvalPostfix is supposed to return the value of the expression. If it is not a legal postfix expression, EvalPostfix must return a special value Infinity which is defined by the judge program.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
typedef double ElementType;
#define Infinity 1e8
#define Max_Expr 30 /* max size of expression */
ElementType EvalPostfix( char *expr );
int main()
{
ElementType v;
char expr[Max_Expr];
gets(expr);
v = EvalPostfix( expr );
if ( v < Infinity )
printf("%f\n", v);
else
printf("ERROR\n");
return 0;
}
/* Your function will be put here */
Sample Input 1:
11 -2 5.5 * + 23 7 / -
Sample Output 1:
-3.285714
Sample Input 2:
11 -2 5.5 * + 23 0 / -
Sample Output 2:
ERROR
Sample Input 3:
11 -2 5.5 * + 23 7 / - *
Sample Output 3:
ERROR
参考答案
#include <string.h> // 包含字符串处理函数
ElementType EvalPostfix(char *expr)
{
/* 栈结构定义 */
ElementType stack[Max_Expr]; // 用于存储操作数的栈
int top = -1; // 栈顶指针,初始化为-1表示空栈
/* 使用strtok分割表达式字符串 */
char *token = strtok(expr, " "); // 首次调用:以空格为分隔符分割字符串
ElementType a, b, result;
while (token != NULL) {
/* 操作符处理分支 */
if (strlen(token) == 1 && strchr("+-*/", token[0])) {
// 有效性检查:栈中至少需要两个操作数
if (top < 1) return Infinity;
// 弹出操作数(注意顺序:先弹出的是第二个操作数)
b = stack[top--]; // 弹出栈顶元素作为右操作数
a = stack[top--]; // 弹出次栈顶元素作为左操作数
// 执行运算
ElementType res;
switch (token[0]) {
case '+':
res = a + b;
break; // 必须添加break防止case穿透
case '-':
res = a - b;
break;
case '*':
res = a * b;
break;
case '/':
if (b == 0) return Infinity; // 除零错误处理
res = a / b;
break;
default:
return Infinity; // 无效操作符(理论上不会执行到这里)
}
// 运算结果入栈
stack[++top] = res;
}
/* 操作数处理分支 */
else {
char *end; // 用于检测转换终止位置的指针
ElementType num = strtod(token, &end); // 字符串转浮点数
// 检查转换有效性:end必须指向字符串末尾
if (*end != '\0') {
return Infinity; // 包含非法字符(如12a3.5)
}
// 数字入栈
stack[++top] = num;
}
// 继续获取下一个token(注意参数变为NULL)
token = strtok(NULL, " ");
}
/* 最终结果检查 */
// 正确情况下栈中应只剩1个元素(计算结果)
return (top == 0) ? stack[0] : Infinity;
}
strtok :
- 函数原型:
char *strtok(char *str, const char *delim) - 功能:分割字符串为标记(token)
- 工作方式:
- 首次调用:传入待分割字符串和分隔符
- 后续调用:传入NULL和分隔符,继续从原字符串分割
- 返回当前标记的指针,没有更多标记时返回NULL
- 示例:
"11 -2 5.5"→ “11” → “-2” → “5.5” → NULL - 注意:会修改原始字符串(将分隔符替换为’\0’)
strlen :
- 函数原型:
size_t strlen(const char *str) - 功能:计算字符串长度(不含终止符’\0’)
- 在本代码中:用于判断操作符token长度是否为1(如”+”是有效操作符,”12”是操作数)
strchr :
- 函数原型:
char *strchr(const char *str, int c) - 功能:在字符串中查找指定字符
- 返回值:找到时返回字符位置指针,否则返回NULL
- 在本代码中:
strchr("+-*/", token[0])检查第一个字符是否为四则运算符
6-6 Level-order Traversal
Write a routine to list out the nodes of a binary tree in “level-order”. List the root, then nodes at depth 1, followed by nodes at depth 2, and so on. You must do this in linear time.
Format of functions:
void Level_order ( Tree T, void (*visit)(Tree ThisNode) );
where void (*visit)(Tree ThisNode) is a function that handles ThisNode being visited by Level_order, and Tree is defined as the following:
typedef struct TreeNode *Tree;
struct TreeNode {
ElementType Element;
Tree Left;
Tree Right;
};
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
#define MaxTree 10 /* maximum number of nodes in a tree */
typedef int ElementType;
typedef struct TreeNode *Tree;
struct TreeNode {
ElementType Element;
Tree Left;
Tree Right;
};
Tree BuildTree(); /* details omitted */
void PrintNode( Tree NodePtr )
{
printf(" %d", NodePtr->Element);
}
void Level_order ( Tree T, void (*visit)(Tree ThisNode) );
int main()
{
Tree T = BuildTree();
printf("Level-order:");
Level_order(T, PrintNode);
return 0;
}
/* Your function will be put here */
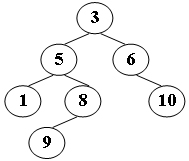
Sample Output (for the tree shown in the figure):
Level-order: 3 5 6 1 8 10 9
参考答案
// 层序遍历
void Level_order ( Tree T, void (*visit)(Tree ThisNode) )
{
if (T == NULL) return; // 处理空树情况
// 使用数组模拟队列,题目中节点数量并不多
Tree queue[MaxTree];
int front = 0; // 头指针
int rear = 0; // 尾指针
queue[rear++] = T; // 根节点入队,尾指针后移
while(front < rear)
{
Tree current = queue[front++]; // 取出队头节点,并出队
visit(current); // 访问队头节点
if(current->Left)
{
queue[rear++] = current->Left; // 左孩子入队
}
if(current->Right)
{
queue[rear++] = current->Right; // 右孩子入队
}
}
}
6-7 Isomorphic
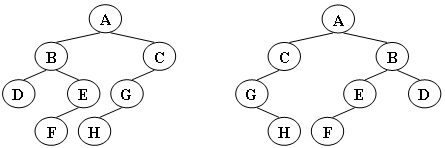
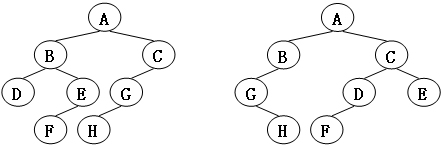
Two trees, T1 and T2, are isomorphic if T1 can be transformed into T2 by swapping left and right children of (some of the) nodes in T1. For instance, the two trees in Figure 1 are isomorphic because they are the same if the children of A, B, and G, but not the other nodes, are swapped.
Give a polynomial time algorithm to decide if two trees are isomorphic.
Format of functions:
int Isomorphic( Tree T1, Tree T2 );
where Tree is defined as the following:
typedef struct TreeNode *Tree;
struct TreeNode {
ElementType Element;
Tree Left;
Tree Right;
};
The function is supposed to return 1 if T1 and T2 are indeed isomorphic, or 0 if not.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
typedef char ElementType;
typedef struct TreeNode *Tree;
struct TreeNode {
ElementType Element;
Tree Left;
Tree Right;
};
Tree BuildTree(); /* details omitted */
int Isomorphic( Tree T1, Tree T2 );
int main()
{
Tree T1, T2;
T1 = BuildTree();
T2 = BuildTree();
printf(“%d\n”, Isomorphic(T1, T2));
return 0;
}
/* Your function will be put here */
Sample Output 1 (for the trees shown in Figure 1):
1
Sample Output 2 (for the trees shown in Figure 2):
0
参考答案
int Isomorphic(Tree T1, Tree T2)
{
// 如果两棵树都为空,则同构
if (T1 == NULL && T2 == NULL)
return 1;
// 如果其中一棵为空而另一棵不为空,则不同构
if ((T1 == NULL && T2 != NULL) || (T1 != NULL && T2 == NULL))
return 0;
// 当前节点的元素必须相同
if (T1->Element != T2->Element)
return 0;
// 递归判断两种情况:不交换左右子树或交换左右子树
return (Isomorphic(T1->Left, T2->Left) && Isomorphic(T1->Right, T2->Right)) ||
(Isomorphic(T1->Left, T2->Right) && Isomorphic(T1->Right, T2->Left));
}
6-8 Percolate Up and Down
Write the routines to do a “percolate up” and a “percolate down” in a binary min-heap.
Format of functions:
void PercolateUp( int p, PriorityQueue H );
void PercolateDown( int p, PriorityQueue H );
where int p is the position of the element, and PriorityQueue is defined as the following:
typedef struct HeapStruct *PriorityQueue;
struct HeapStruct {
ElementType *Elements;
int Capacity;
int Size;
};
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
typedef int ElementType;
#define MinData -1
typedef struct HeapStruct *PriorityQueue;
struct HeapStruct {
ElementType *Elements;
int Capacity;
int Size;
};
PriorityQueue Initialize( int MaxElements ); /* details omitted */
void PercolateUp( int p, PriorityQueue H );
void PercolateDown( int p, PriorityQueue H );
void Insert( ElementType X, PriorityQueue H )
{
int p = ++H->Size;
H->Elements[p] = X;
PercolateUp( p, H );
}
ElementType DeleteMin( PriorityQueue H )
{
ElementType MinElement;
MinElement = H->Elements[1];
H->Elements[1] = H->Elements[H->Size--];
PercolateDown( 1, H );
return MinElement;
}
int main()
{
int n, i, op, X;
PriorityQueue H;
scanf("%d", &n);
H = Initialize(n);
for ( i=0; i<n; i++ ) {
scanf("%d", &op);
switch( op ) {
case 1:
scanf("%d", &X);
Insert(X, H);
break;
case 0:
printf("%d ", DeleteMin(H));
break;
}
}
printf("\nInside H:");
for ( i=1; i<=H->Size; i++ )
printf(" %d", H->Elements[i]);
return 0;
}
/* Your function will be put here */
Sample Input:
9
1 10
1 5
1 2
0
1 9
1 1
1 4
0
0
Sample Output:
2 1 4
Inside H: 5 10 9
参考答案
// 向上渗透
void PercolateUp(int p, PriorityQueue H) {
// 暂存刚插入的元素
ElementType temp = H->Elements[p];
// 从刚插入节点开始向上寻找父节点,从下往上遍历
while (p > 1) {
int parent = p / 2;
// 如果刚插入的元素小于当前位置的父节点,父节点元素下移,指针上移
if (temp < H->Elements[parent]) {
H->Elements[p] = H->Elements[parent];
p = parent;
} else {// 如果出现刚插入的节点大于父节点,则不能向上调整
break;
}
}
// 当退出循环后,p在刚插入节点应该在的位置,将暂存元素保存到根节点
H->Elements[p] = temp;
}
void PercolateDown(int p, PriorityQueue H) {
// 暂存删除的元素
ElementType temp = H->Elements[p];
int child;
// 没有溢出,从上往下遍历
while (p * 2 <= H->Size) {
// 寻找子节点位置
child = p * 2;
// 没溢出且找到左右节点较小的那个
if (child != H->Size && H->Elements[child + 1] < H->Elements[child]) {
child++;
}
// 如果子节点小于要删除的节点,子节点上移
if (H->Elements[child] < temp) {
H->Elements[p] = H->Elements[child];
p = child;
} else {
break;
}
}
// 此时找到最下方的位置,将暂存的要删除的元素保存到最下方
H->Elements[p] = temp;
}
6-9 Sort Three Distinct Keys
Suppose you have an array of N elements, containing three distinct keys, “true”, “false”, and “maybe”. Given an O(N) algorithm to rearrange the list so that all “false” elements precede “maybe” elements, which in turn precede “true” elements. You may use only constant extra space.
Format of functions:
void MySort( ElementType A[], int N );
where ElementType A[] contains the N elements.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
typedef enum { true, false, maybe } Keys;
typedef Keys ElementType;
void Read( ElementType A[], int N ); /* details omitted */
void MySort( ElementType A[], int N );
void PrintA( ElementType A[], int N )
{
int i, k;
k = i = 0;
for ( ; i<N && A[i]==false; i++ );
if ( i > k )
printf("false in A[%d]-A[%d]\n", k, i-1);
k = i;
for ( ; i<N && A[i]==maybe; i++ );
if ( i > k )
printf("maybe in A[%d]-A[%d]\n", k, i-1);
k = i;
for ( ; i<N && A[i]==true; i++ );
if ( i > k )
printf("true in A[%d]-A[%d]\n", k, i-1);
if ( i < N )
printf("Wrong Answer\n");
}
int main()
{
int N;
ElementType *A;
scanf("%d", &N);
A = (ElementType *)malloc(N * sizeof(ElementType));
Read( A, N );
MySort( A, N );
PrintA( A, N );
return 0;
}
/* Your function will be put here */
Sample Input:
6
2 2 0 1 0 0
Sample Output:
false in A[0]-A[0]
maybe in A[1]-A[2]
true in A[3]-A[5]
参考答案
// low指针管理false,mid指针用于遍历,high指针用于管理true
// 将false放前边,true放后边,剩下的maybe就在中间了。
// 所以从头开始遍历,遇到false放前边,low指针右移,同时mid指针右移
// 因为是与前边交换,指针是从前边遍历过来的,只能是false和maybe互换,如果前边有true,已经换到了后边
// 如果遇到true,与high指针互换,high指针左移,但mid指针不动,因为high指的可能是maybe或者false
// 所以重新检查mid位置的元素是什么,继续遍历,
// 直到mid到high的位置遍历最后一个,如果这个是false,需要将它移动到前边,mid大于high之后遍历完毕
void MySort(ElementType A[], int N) {
int low = 0, mid = 0, high = N - 1;
while (mid <= high) {
if (A[mid] == false) { // false的枚举值为1
// 交换到false区域
ElementType temp = A[low];
A[low] = A[mid];
A[mid] = temp;
low++;
mid++;
} else if (A[mid] == maybe) { // maybe的枚举值为2
// 留在中间区域
mid++;
} else { // true的枚举值为0
// 交换到true区域
ElementType temp = A[mid];
A[mid] = A[high];
A[high] = temp;
high--;
}
}
}
6-10 Strongly Connected Components
Write a program to find the strongly connected components in a digraph.
Format of functions:
void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) );
where Graph is defined as the following:
typedef struct VNode *PtrToVNode;
struct VNode {
Vertex Vert;
PtrToVNode Next;
};
typedef struct GNode *Graph;
struct GNode {
int NumOfVertices;
int NumOfEdges;
PtrToVNode *Array;
};
Here void (*visit)(Vertex V) is a function parameter that is passed into StronglyConnectedComponents to handle (print with a certain format) each vertex that is visited. The function StronglyConnectedComponents is supposed to print a return after each component is found.
Sample program of judge:
#include <stdio.h>
#include <stdlib.h>
#define MaxVertices 10 /* maximum number of vertices */
typedef int Vertex; /* vertices are numbered from 0 to MaxVertices-1 */
typedef struct VNode *PtrToVNode;
struct VNode {
Vertex Vert;
PtrToVNode Next;
};
typedef struct GNode *Graph;
struct GNode {
int NumOfVertices;
int NumOfEdges;
PtrToVNode *Array;
};
Graph ReadG(); /* details omitted */
void PrintV( Vertex V )
{
printf("%d ", V);
}
void StronglyConnectedComponents( Graph G, void (*visit)(Vertex V) );
int main()
{
Graph G = ReadG();
StronglyConnectedComponents( G, PrintV );
return 0;
}
/* Your function will be put here */
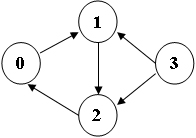
Sample Input (for the graph shown in the figure):
4 5
0 1
1 2
2 0
3 1
3 2
Sample Output:
3
1 2 0
Note: The output order does not matter. That is, a solution like
0 1 2
3
is also considered correct.
参考答案
static void DFS(Vertex u, Graph G, int *visited, Vertex *stack, int *top) {
visited[u] = 1;
PtrToVNode node = G->Array[u];
while (node != NULL) {
Vertex v = node->Vert;
if (!visited[v]) {
DFS(v, G, visited, stack, top);
}
node = node->Next;
}
stack[++(*top)] = u;
}
static void DFS2(Graph G, Vertex u, int *visited, void (*visit)(Vertex)) {
visited[u] = 1;
visit(u);
PtrToVNode node = G->Array[u];
while (node != NULL) {
Vertex v = node->Vert;
if (!visited[v]) {
DFS2(G, v, visited, visit);
}
node = node->Next;
}
}
void StronglyConnectedComponents(Graph G, void (*visit)(Vertex V)) {
Vertex stack[MaxVertices];
int top = -1;
int visited[MaxVertices] = {0};
// 第一次DFS遍历原图,得到逆后序栈
for (int u = 0; u < G->NumOfVertices; u++) {
if (!visited[u]) {
DFS(u, G, visited, stack, &top);
}
}
// 构造转置图
Graph transposeG = (Graph)malloc(sizeof(struct GNode));
transposeG->NumOfVertices = G->NumOfVertices;
transposeG->NumOfEdges = G->NumOfEdges;
transposeG->Array = (PtrToVNode *)malloc(transposeG->NumOfVertices * sizeof(PtrToVNode));
for (int i = 0; i < transposeG->NumOfVertices; i++) {
transposeG->Array[i] = NULL;
}
for (int u = 0; u < G->NumOfVertices; u++) {
PtrToVNode node = G->Array[u];
while (node != NULL) {
Vertex v = node->Vert;
PtrToVNode newNode = (PtrToVNode)malloc(sizeof(struct VNode));
newNode->Vert = u;
newNode->Next = transposeG->Array[v];
transposeG->Array[v] = newNode;
node = node->Next;
}
}
// 第二次DFS遍历转置图,按栈的顺序处理
int visited2[MaxVertices] = {0};
for (int i = top; i >= 0; i--) {
Vertex u = stack[i];
if (!visited2[u]) {
DFS2(transposeG, u, visited2, visit);
printf("\n");
}
}
// 释放转置图内存
for (int i = 0; i < transposeG->NumOfVertices; i++) {
PtrToVNode node = transposeG->Array[i];
while (node != NULL) {
PtrToVNode tmp = node;
node = node->Next;
free(tmp);
}
}
free(transposeG->Array);
free(transposeG);
}